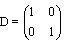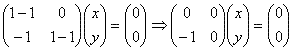Matriz identidad: Matriz cuadrada que tiene en cada una de las entradas de su diagonal principal el valor 1 y en el resto 0.
Ejemplos de matriz Identidad de orden 2 (2x2), orden 3 (3x3) y orden 4 (4x4).
Polinomio característico: Se obtendrá de aplicar el determinante l A-λI l=0 e igualando a cero para obtener las soluciones o raíces.
Matriz de Paso: Matriz que se forma de los autovectores o vectores propios puestos en columna.
Autovalores o valores propios: Son las soluciones que se obtienen del polinomio característico y pueden tener multiplicidad mayor de 1.
Autovectores o vectores propios: Son los vectores no nulos, que obtenemos a partir de los valores propios obtenidos en el polinomio característico. La forma de obtener los vectores es usando la forma:
Ejemplo de como podemos obtener un autovector a partir de un autovalor
Supongamos que tenemos el autovalor λ = -1 de la matriz :
Como sabemos que λ = -1 sustituimos en la matriz y resolvemos, quedando un sistema de ecuaciones, donde se aprecia que son la misma ecuación:
2 V1 + 2 V2 = 0
2 V1 + 2 V2 = 0
2 V1 + 2 V2 = 0
Eliminaremos una ecuación y resolvemos quedándonos que V1 = -V2, con lo que podemos determinar el vector propio asociado al valor propio λ = -1, siendo este:
(-V2 , V2 ) = V2 ( -1 , 1 ) , El vector propio es ( -1 , 1 )
Diagonalización de Matrices de orden 2 (2x2).
Vamos a comenzar diagonalizando una matriz no simétrica de orden 2, como por ejemplo:
Pasos a seguir:
Obtendremos el polinomio característico de la matriz mediante l A-λI l=0
Solucionamos el determinante obteniendo:
(1-λ) (-2-λ) = 0 → λ ² + λ - 2 = 0
El polinomio característico sería λ ² + λ - 2 = 0 y nos da como resultado λ = 1 y λ = -2, siendo estos los autovalores o valores propios asociados a la matriz A.
Puesto que los autovalores son distintos, ya podríamos predecir que la matriz será diagonalizable. Ademas ya podríamos construir la matriz diagonal a partir de sus valores propios.
Continuamos ahora con el cálculo de autovectores o vectores propios, para ello usaremos la forma:
Para el valor propio: λ = 1.
Como resultado obtenemos la ecuación:
x -3y = 0 → x = 3y
sustituimos en ( x , y ) y obtenemos
(x,y) → (3y , y) = y (3 , 1)
Siendo el autovector: (3 , 1)
Para el valor propio: λ = -2
Como resultado obtenemos la ecuación:
3x = 0 → x = 0
sustituimos en ( x , y ) y obtenemos
(x,y) → (0 , y) = y (0 , 1)
Siendo el autovector: (0 , 1)
La matriz de paso y su inversa serán :
Teniendo la matriz diagonal, la de paso y su inversa, vemos si se cumple:
Obtenemos el polinomio característico de la matriz mediante l A-λI l=0
Solucionamos el determinante obteniendo:
(1-λ) (1-λ) - 0 = 0 → (1-λ) (1-λ) = 0, las soluciones en este caso se nos dan directas sin necesidad de hacer ningún calculo, siendo λ = 1 con multiplicidad = 2, al tener un autovalor que se repite en este caso no podemos predecir que la matriz será diagonalizable, sino que debemos calcular los vectores propios para saber, si es o no, diagonalizable.
Construimos su matriz diagonal:
Calculamos autovectores o vectores propios, usando la forma:
Para el valor propio: λ = 1
Como resultado, obtenemos la ecuación:
-x = 0 → x = 0
(x,y) → (0, y) = y (0 , 1)
Diagonalización de Matrices de orden 3 (3x3).
Primero elegimos una matriz cuadrada de 3x3, que llamaremos A.
Los pasos a seguir serán, primero calcular su matriz diagonal a partir de sus autovalores o valores propios y encontrar la matriz de paso que se genera a partir de los autovectores o vectores propios.
1. Cálculo de los valores propios mediante el polinomio característico, usaremos l A-λI l=0
Solucionando el determinante obtenemos que (1-λ) (2-λ) (3-λ) = 0 de aquí se desprenden de forma directa, los autovalores, que determinan la matriz diagonal y nos auguran que la matriz será diagonalizable, ya que todos sus autovalores poseen multiplicidad 1, o sea, que no se repiten.
2. Cálculo de los vectores propios o autovectores. De la misma forma que hicimos en la matriz de 2x2.
Comenzamos a calcular los vectores propios con el autovector λ=1
Resolviendo obtenemos dos ecuaciones.
x + y + 3z = 0 → x = -y
2z = 0 → z = 0
sustituimos en ( x , y , z ) y obtenemos
( x , y , z ) → (-y , y , 0 ) → y (-1 , 1 , 0 )
Ya hemos conseguido el primer autovector : ( -1 , 1 , 0 )
Continuamos con el autovector o vector propio λ = 2
Resolviendo obtenemos dos ecuaciones.
-x = 0 → x = 0
z = 0 → z = 0
sustituimos en ( x , y , z ) y obtenemos
( x , y , z ) → (0 , y , 0 ) → y (0 , 1 , 0 )
el segundo vector propio : ( 0 , 1 , 0 )
El último autovector o vector propio λ = 3
El último autovector o vector propio λ = 3
Resolviendo obtenemos dos ecuaciones.
-2x = 0 → x = 0
x -y + 3z = 0 → y = 3z
sustituimos en ( x , y , z ) y obtenemos
( x , y , z ) → (0 , 3z , z ) → z (0 , 3 , 1 )
El tercer vector propio sería: (0 , 3 , 1 )
Al obtener los tres autovectores, podemos construir la matriz de paso, colocando los vectores propios en columna.
Diagonalización de Matrices de orden 4 (4x4).
Vamos a escoger una matriz 4x4, por ejemplo esta:
Para el cálculo de autovectores y vectores propios, procederemos igual que en los casos de orden 2 y orden 3. Así que a partir de l A-λI l=0 obtendrenos los valores propios y podremos construir la matriz diagonal.
Aplicando la propiedad de los determinantes, ya que la primera columna esta compuesta de ceros excepto un valor, de esta forma queda un determinante de 3x3 mas sencillo de resolver. Aunque podríamos reducirlo mas, lo solucionaremos con esta forma.
Al solucionarlo nos queda (1-λ) (1-λ) (2-λ) (-1-λ) = 0, teniendo sus cuatro autovalores, ya podríamos construir la matriz diagonal. Como tenemos que λ = 1 tiene multiplicidad 2, este sera el primer valor propio en verificar, pues necesitamos obtener dos vectores de él.
Para λ = 1
2y - z + t = 0
2y - z + t = 0
Resolviendo obtenemos tres ecuaciones.
y = 0
z = 0
z -2t = 0 → t = 0
sustituimos en ( x , y , z , t ) y obtenemos
( x , y , z , t ) → (x , 0 , 0 , 0 ) → x (1 , 0 , 0 , 0 )
Puesto que solo hemos obtenido un vector y necesitábamos dos la matriz no será diagonalizable.
----------------------------------------------------
Vamos a diagonalizar otra matriz, por ejemplo.
Calculamos sus autovalores a partir de l A-λI l=0
Aplicando la propiedad de los determinantes, nos queda:
Al solucionar el determiante obtenemos (1-λ) (-1-λ) (2-λ) (-1-λ) = 0, teniendo sus cuatro autovalores, ya podríamos construir la matriz diagonal. Como tenemos que λ = -1 tiene multiplicidad 2, este sera el primer valor propio en verificar.
Para λ = -1
Resolviendo obtenemos dos ecuaciones.
2x + 2y - z + t = 0 → t = -2x -2y
3z = 0 → z = 0
sustituimos en ( x , y , z , t ) y obtenemos
( x , y , z , t ) → (x , y , 0 , -2x -2y) →
→(x , 0 , 0 , -2x ) + ( 0 , y , 0 , -2y) = x (1 , 0 , 0 , -2 ) + y( 0 , 1 , 0 , -2)
Hemos obtenido dos autovectores V2 (1 , 0 , 0 , -2 ) y V4 ( 0 , 1 , 0 , -2), el hecho de que sean V2 y V4 lo explico mas adelante.
Para λ = 2
Resolviendo obtenemos tres ecuaciones.
-x + 2y - z + t = 0 → x = -z
-3y = 0 → y = 0
-3t = 0 → t = 0
sustituimos en ( x , y , z , t ) y obtenemos
( x , y , z , t ) → (-z , 0 , z , 0) → z (-1 , 0 , 1 , 0)
Hemos obtenido otro autovector V3 (-1 , 0 , 1 , 0 )
Para λ = 1
Resolviendo obtenemos tres ecuaciones.
-2y = 0 → y = 0
z = 0 → z = 0
-2t = 0 → t = 0
sustituimos en ( x , y , z , t ) y obtenemos
( x , y , z , t ) → (x , 0 , 0 , 0) → x (1 , 0 , 0 , 0)
Hemos obtenido otro autovector V1 (1 , 0 , 0 , 0 )
La matriz de paso será:
Los vectores propios de la matriz de paso se colocan en la columna exacta donde están los valores propios que los generan, por este motivo que los dos primeros vectores que haya obtenido sean V2 y V4 no es al azar, es porque el autovalor que los genera esta en la columna dos y cuatro de la matriz diagonal. Os pongo la matriz diagonal para que veáis donde he situado los autovalores.
Para comprobar si el ejercicio esta bien y poder asegurar que la matriz es diagonalizable necesitamos la matriz de paso inversa, que sería esta:
Y por último la comprobación:
Si hacéis las operaciones comprobareis que da como resultado la matriz M, puesto que esta matriz es diagonalizable.